Tracé d'une ligne

Je vais vous présenter ici 3 méthodes permettant le tracé d'une ligne en utilisant des entiers. Ces méthodes permettent de travailler directement sur la mémoire, par exemple dans un DIB moyennant un clipping préalable et sont donc très rapides.

1. Algorithme de Jack Bresenham (identification des coordonées idéales)
2. 1er Algorithme de Nicolas Rey (Représentation fractale)
3. 2ème Algorithme de Nicolas Rey (Dénombrement)

Algorithme de Jack Bresenham

On parcourt la plus grande dimension du rectangle contenant la ligne et pour chaque pixel le calcul d'erreur minimale est calculé ce qui permet d'opter pour le pixel étant le plus proche d'une ligne logique (contenant la plus grande longueur de la portion de ligne contenu dans le pixel). Jack Bresenham est le premier a avoir implémenté un algorithme de tracé de segment en 1962 chez IBM afin de piloter un traceur. Son algorithme prend en compte la prérogative d'avoir le point de départ et d'arrivée de la ligne au milieu du pixel, nécessité imposée par le tracage.

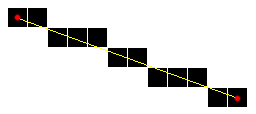
Implémentation

DrawLineBresenham

1er Algorithme de Nicolas Rey

Le calcul d'erreur minimale étant cette fois initié avant la boucle. Bien qu'il ressemble à s'y méprendre à l'algorythme de Bresenham il en diffère pourtant radicalement pour 2 raisons :

1. Le raisonnement qui à conduit à son élaboration se base sur une représentation fractale et non sur sa position logique supposée.
2. La ligne logique va de x1 à x2+1 de Y1 à Y2+1 et sa représentation à l'écran diffère donc de la ligne logique de l'algorithme de Bresenham qui va de x1+0.5 à X2-0.5 et de Y1+0.5 à Y2-0.5. Ces postulats sont arbitraires et ne dépendent que de l'objectif du programmeur. Jack E. Bresenham ayant créé son algorithme dans le but de piloter un traceur son option d'aller d'un milleu de pixel à un autre est donc tout à fait compréhensible. Notons cependant que la longueur de la ligne logique dans mon algorythme correspond extactement à la longueur physique à l'écran.

Théorie : L'écran étant une mosaique de carrés, on va donc tracer une abstraction de la ligne. Etant donné des coordonnées entières, on connait la largeur et la hauteur de la zone de tracage. On peut donc avoir une vision fractale en englobant ce rectangle dans un carré dont le coté est égal au plus grand coté du rectangle. On sait maintenant qu'on peut juxtaposer une suite de rectangles en connaissant les coordonnées entières et leur positions dans un damage virtuel. 

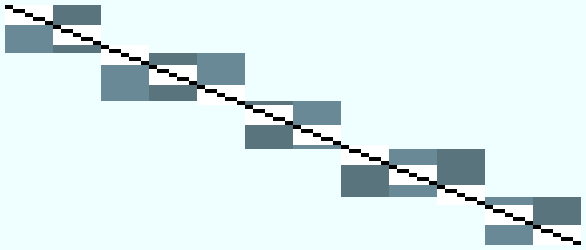
Implémentation

DrawLineFractalNicolasRey

2ème Algorithme de Nicolas Rey

Comme dit plus haut on ne dessine pas une ligne mais une mosaïque représentant une abstraction de cette ligne. On sait donc qu'on aura une succession de segments de longueurs différentes mais ayant assurément 1 pixel d'écart.  On va donc calculer le nombre de segments de longueur N et de longueur N+1, puis les répartir en utilisant une comparaison de fraction optimisée. L'avantage avec cette méthode est qu'il n'y a pas de calcul autre que l'incrémentation pour chaque segments. Avantage moindre lorsque la ligne se trouve fortement inclinée puisqu'on effectue la comparaison à chaque changement de ligne/colonne.

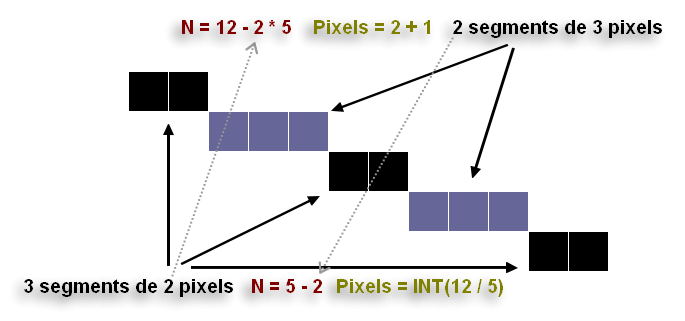
Implémentation

DrawLineCountingNicolasRey