Restriction d'une ligne à une région (Line Clipping)

schéma d'un zone de clipping

Voici les 5 algorithmes de "Line-Clipping" les plus performants que je connaisse par ordre de performance décroissant .

Algorithme de Nicolas Rey

Le plus simple et le plus rapide, il supplante tous les algorithmes existants en terme de rapidité. Basé sur une réduction en 4 temps.

Algorithme de K.R. Wijeweera/S.R Kodituwakku/M.A.P Chamikara (gradiant de pente)

Cet algorithme absolument remarquable a été présenté en 2012 dans le "Ceylon Journal of Science" par 3 Sri-Lankais : Kasun Ranga Wijeweera, Saluka Ranasinghe Kodituwakku et Mahawaga Arachchige Pathum Chamikara. Il est plus rapide que ceux de Cohen/Sutherland et de Liang/Barsky. Son élaboration se base sur l'observation de la coincidence des 2 points d'un segment extérieur à la zone de clipping après élagage.Il aurait été supplanté de peu par celui de Matthes/Drakopoulos en 2019 (Another simple but faster method for 2D Line Clipping) cependant je l'ai moi-même testé et j'émet un gros doute sur leur résultat. Soit l'algorithme présenté n'est pas celui qui a été utilisé soit leur benchmark présente un défaut. En ce qui me concerne je considère l'algorithme W.K.C. comme étant toujours le plus performant après le mien.

Algorithme de Liang/Barsky (équation paramétrique)

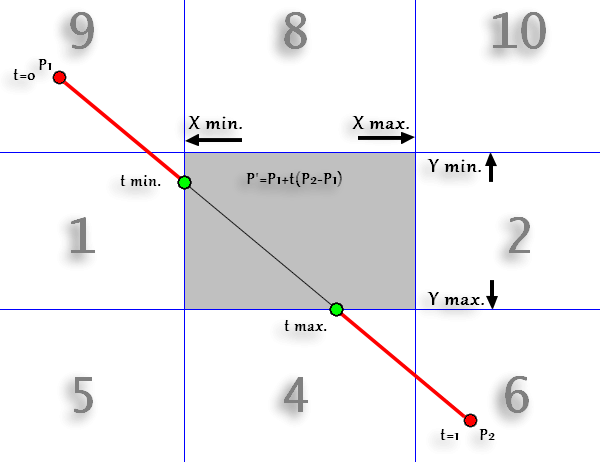
Cette approche astucieuse définit la ligne par P1+t*(P2-p1) avec 0≤t≤1 ce qui permet de tester chaque coté du rectangle de découpage avec 2 paramètres P et Q correspondants aux dimensions :

gauche : p = -(x2-x1), q = x1 - xmin
droite : p = (x2-x1) , q = xmax - x1
haut : p = -(y2-y1), q = y1 - ymin
bas : p = (y2-y1) , q = ymax - y1

Si p = 0 la ligne est parrallèle à un autre coté
Si q < 0 La ligne est complètemt extérieure
Si q >= 0 La ligne passe par l'intérieur
si p > 0 la ligne va vers l'extérieur
si p < 0 la ligne va vers l'intérieur

Le paramètre t de l'équation peut être calculé avec q/p. Il ne reste qu'à sélectionner le t minimum et le t maximum.

Algorithme de Cohen/Sutherland (9 zones)

Le plus ancien et connu des algorithmes de "Line-Clipping", conçu en 1967 lors du développement du fameux jeu "Flight-Simulator" par Danny Cohen et  Ivan Sutherland. Il se base sur un découpage du plan en 9 zones. Chacun des 2 points du segment à découper est classé selon la zone où il se trouve grâce à un code binaire. Ce code détermine la découpe à effectuer et le code du point modifié est changé. On recommence alors jusqu'à ce que les codes indiquent qu'aucune découpe n'est nécessaire. Il existe une version améliorée de cet algorithme (voir https://www.sciencedirect.com/science/article/abs/pii/0097849387900616), que j'e n'ai pas implémenté pour l'instant, qui consiste à coder la ligne complète, c.a.d. regrouper les 2 codes en 1 et à switcher directement sur l'opération conséquente. D'après ce document  on passerait devant l'algorithme de Liang-Barsky en terme de rapidité.

Algorithme de Dimitrios Matthes / Vasileios Drakopoulos

Très simple et sensé être très rapide d'après ce document : https://aircconline.com/ijcga/V9N3/9319ijcga01.pdf. Malheureusement je n'ai pas trouvé l'implémentation C++ ce qui m'aurait aidé à comprendre pourquoi j'obtiens un résultat très décevant avec mon code GFA-Basic 32.

Implémentation des 5 algorithmes

BenchmarkLineClipping

Epilogue

Pour l'instant aucun des algorithmes existants n'atteint le minimum théorique du nombre d'opérations, à savoir que seuls 2 calculs seraient nécessaires. Je subodore qu'une approche par discrimination de sens avec Sgn((x2 - x1) * (py - y1) - (y2 - y1) * (px - x1)) permetrais de cibler l'opération en question, avec quelques optimisation de redondances. J'y reviendrais peut-être, en attendant je vais me pencher sur le clipping de cercle.

Comments est propulsé par CComment