Il existe 2 définitions principales de l'ellipse qui sont valables :
- C'est une courbe résultante de l'intersection d'un plan et d'une surface conique, plus généralement un cylindre.
- C'est l'ensemble des points dont la somme des distances à 2 points fixes appelés "foyers" est constante.
Le site de Gérard Villemin lui consacre une page très intéressante : http://villemin.gerard.free.fr/Geometri/Coniques/Ellipse.htm
J'ajoute une troisième définition complémentaire :
- C'est un cercle qui subit une déformation en X et Y puis une rotation. Elle peut être définie par un centre (Cx,Cy) 2 rayons (Rx,Ry) et une orienation Ao. C'est cette définition que je vais utiliser pour une raison pratique : Effectuer des calculs applicables à l'UDT D2D1_ARC_SEGMENT de la librairie Direct2D.
Il faut aussi que je précise ce que j'appelle une corde de l'ellipse : Une corde est un segment reliant 2 points quelconque de l'ellipse, donc de longueur variable.
Les points d'apogée et médium d'une ellipse

Les points d'apogées sont situés au plus haut et au plus bas de l'ellipse. Les points médium délimitent les régions de même aires de l'ellipse de part et d'autre de l'axe des abscisses. J'ai écrit ces 2 fonctions qui permettent d'obtenir leurs coordonnées. Pour l'apogée je soustrait l'angle du rayon déformé de l'ellipse à celui de l'ellipse elle-même pour calculer la rotation inverse à effectuer. Pour le point médium j'utilise une version réduite de l'intersection de l'ellipse avec l'axe des abscisses (X). Ces 4 points définissent une norme isométrique de déformation du cercle, cela permet de calculer la position d'une corde de longueur arbitraire.
EllipseApogee
EllipseMedium
Dessiner une ellipse
Procédure permettant de dessiner une ellipse conforme à l'algorithme Direct2D, à titre plus indicatif qu'utile.
DrawEllipse
Intersection de l'ellipse avec une ligne
L'algorithme se base sur l'intersection d'une ligne et d'un cercle. La ligne est déformée et tournée en fonction inverse de l'ellipse. Le point d'intersection du cercle est ensuite retourné puis déformé pour correspondre à l'ellipse. La fonction return "True" en cas d'intersection, les coordonnées des 2 points d'intersections sont alors retournées par ix1,iy1,ix2,iy2.
IntersectionLineEllipse
Distance d'un point à une ellipse
Pour cette fonction j'ai utilisé une discrimination dichotomique sur les 2 moitiés de l'ellipse. Afin de pouvoir renvoyer une distance négative si le point est à l'intérieur de l'ellipse je calcule la position des foyers pour avoir la distance du point à ces foyers. Si la somme des distances est supérieure ou inférieure à la longueur de la corde de tracage de l'ellipse le point est à l'extérieur ou à l'intérieur de celle-ci.
DistancePointEllipse
Calculer la position d'une corde
La position d'une corde d'une pente donnée (angle et longueur fixes) dans une ellipse peut être trouvée à 1 ou 2 endroits.
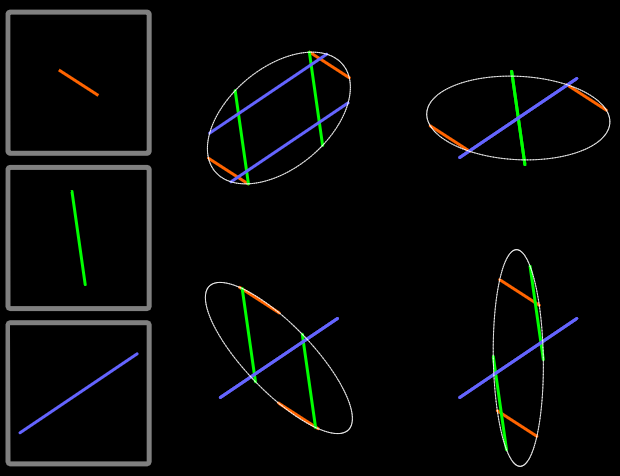
On exclue 4 cas particuliers en centrant simplement la corde plutôt que de déclencher une erreur :
- Rx=0
- Ry=0
- Longueur de la corde = 0
- Longueur de la corde supérieure à la section de l'ellipse
Etapes de calculs :
- Rotation de l'ellipse suivant l'angle de la corde pour simplifier la suite.
- Calcul du point d'apogée et de la longueur de la médiane en y=0.
- Factoriser la longueur vers l'apogée en utilisant le rapport médiane/corde.
- Reporter la longueur de la corde en x puis effectuer la rotation inverse.
- Retouner l'échelle d'agrandissement ou de réduction nécessaire pour un ArcSegment Direct2D.
EllipseCordePosition
Ellipse de l'ArcSegment Direct2D
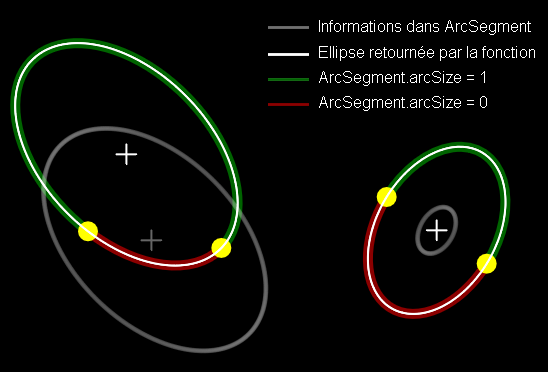
Finalement la position de l'ellipse de l'ArcSegment Direct2D peut être déduite en retrouvant la position du segment avec la fonction EllipseCordePosition() qui nous donne l'offset de déplacement de l'ellipse ainsi que son échelle d'agrandissement nécessaire.
EllipseOfArcSegment

Comments est propulsé par CComment